Análisis semántico vectorial
Contents
6. Análisis semántico vectorial#
Borja Navarro Colorado
Nota
Para completar este tema debéis leer el capítulo 6 “Vector Semantics and Embeddings” del libro de Jurafsky y Martin (2023) Speech and language processing, donde se amplía y se dan detalles (sobre todo matemáticos) de las ideas aquí expuestas. Debes leer hasta la sección 6.6. Lee también la sección 6.8 (“word2vec”), pero no te preocupes si algún concepto no queda claro porque en temas siguientes se volverá a esto. El resto del capítulo es lectura opcional.
Como lectura opcional para profundizar en cómo un vector puede representar el significado de palabras y oraciones, os recomiendo este artículo:
Peter D. Turney y Patrick Pantel (2010) “From Frequency to Meaning: Vector Space Models of Semantics” en Journal of Artificial Intelligence Research, 37, págs. 141-188. DOI: https://doi.org/10.1613/jair.2934
https://www.jair.org/index.php/jair/article/view/10640
https://www.jair.org/index.php/jair/article/view/10640/25440
6.1. Objetivos#
En este tema se expone la semántica distribucional, modelo semántico en el que se basan los actuales sistemas de deep learning. Tras definir la semántica distribucional, se mostrará cómo se puede representar el significado mediante vectores, los principales factores que determinan la representación vectorial y finalmente los conceptos de distancia y similitud textual.
6.2. Introducción#
La semántica vectorial es un aproximación formal a la semántica de las lenguas naturales. A diferencia de otros modelos computacionales, el formalismo está basado en espacios vectoriales y álgebra lineal; y la interpretación de un texto se expresa en términos geométricos de distancia y similitud (Widdows 2004).
Desde un punto de vista lingüístico, el modelo semántico vectorial representa el significado distribucional de las palabras. Como se comentará luego, el significado distribucional es aquél que podemos derivar a partir del contexto en el que una palabra es utilizada. En este modelo, el significado no es una unidad atómica como en lógica forma ni está definido en un diccionario, sino que es el propio uso de cada palabra en los diferentes contextos donde suele aparecer.
6.3. Origen computacional#
La aplicación de modelos vectoriales para procesar texto proviene del área llamada Recuperación de información (Information Retrieval). En esta área se desarrollan sistemas que, dada una consulta, recupera un conjunto de documentos ordenados de mayor a menor relevancia. El producto más conocido desarrollado en esta área son los buscadores de internet.
Para determinar la relación de la consulta (conjunto de palabras) con los documentos, éstos se representan mediante una matriz término-documento. En este matriz, cada palabra está representada por su relevancia en cada documento (por ejemplo, mediante su frecuencia). Así, dada una palabra (en la cosulta), se pude derivar en qué documentos esa palabra es más relevante. Estos modelos se llaman también ``modelos de bolsa de palabras’’ (bag of words) porque las palabras se tratan como un conjunto sin orden ni relación entre ellas. En su estado mas básico se ignora la información categorial, sintáctica, etc. del texto.
En esta matriz, por tanto, cada columna representa un documento y cada línea una palabra o término. El valor de cada celda es la relevancia del término o palabra en el documento. Aquí se pueden aplicar varios fórmulas para determinar esa relevancia, que se verán después. La más básica sería la frecuencia relativa del término en el documento. De esta manera, cada columna es un vector que representa un texto, y cada línea es un vector que representa los contextos de aparición de una palabra (cada documento es aquí un contexto de uso). La siguiente matriz representa las frecuencias absolutas de las palabras de dos documentos (doc1 y doc2), cada uno con tres palabras.
doc1 \(= \{casa, madera, mesa\}\)
doc2 \(= \{papel, rama, madera\}\)
Doc 1 Doc 2
casa 1 0
madera 1 1
mesa 1 0
papel 0 1
rama 0 1
De esta tabla se obtiene la siguiente matriz D:
De esta manera, los documentos ahora está representado como dos vectores:
\(\vec{doc1} = \{1 1 1 0 0\}\)
\(\vec{doc2} = \{0 1 0 1 1\}\)
Y cada palabra o término está representado con su vector contextual:
\(\vec{casa} = \{1 0\}\)
\(\vec{madera} = \{1 1\}\)
\(\vec{mesa} = \{1 0\}\)
\(\vec{papel} = \{0 1\}\)\
\(\vec{rama} = \{0 1\}\)
6.4. Fundamentos lingüísticos#
Los modelos semánticos vectoriales asumen básicamente tres propuestas teóricas (Clarke 2011):
La idea de Wittgenstein (1953) de que “meaning just is use” (Wittgenstein 1953);
El concepto de collocation de Firth (1957) y su idea de que
“you shall know a word by the company it keeps”;
La hipótesis distribucional de Harris (1968), según la cual:
“words will occur in similar contexts if and only if they have similar meanings”.
Todo ello se engloba dentro del concepto de “significado distribucional”. Este, por tanto, es el significado que una palabra asume cuando se usa en un contexto concreto y queda determinado a partir de las palabras de ese contexto con las que aparece. Esta inferencia semántica (determinar el significado de una palabra a partir de las palabras del contexto) es algo que hacemos constantemente. Mira las siguientes oraciones, ¿qué significado tiene XXX en cada una?
Mañana iré al XXX a firmar la hipoteca, y ya de paso sacaré dinero del cajero.
He intentado ponerme los XXX de mi hermano pero me vienen pequeños: mis pies son muy grandes y necesito una talla más.
6.5. Representación vectorial del significado#
El vector de una palabra como se ha mostrado antes representa el significado distribucional de una palabra ya que captura la relevancia de esa palabra (o término o token o lema, según se quiera llamar) en cada uno de los contextos (en este caso documentos) que forman la colección. Así, en la siguiente matriz término - documento:
doc1 doc2
car 7 6
taxi 5 6
train 6 1
el significado de cada palabra sería el vector contextual:
\(car = (7,6)\)
\(taxi = (5,6)\)
\(train = (6,1)\)
Esto se puede representar en un espacio euclídeo (plano o lineal) mediante coordenadas cartesiana: los valores del vector se proyectan en los ejes de coordenadas, siendo la abscisa \(x\) el documento 1 la ordenada \(y\) el documento 2.
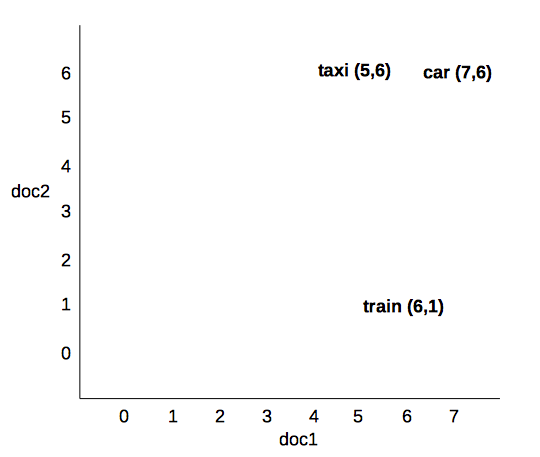
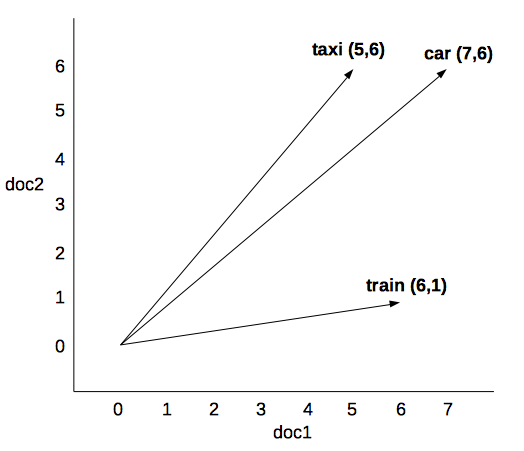
Esto en un plano cartesiano de dos dimensiones. Si la colección está formada por \(n-\) documentos, obtendríamos un espacio \(n\)-dimensionales o multidimensionales en el que cada dimensión es un posible contexto.
Para que este modelo vectorial represente el significado real de las palabras, hay que modelar bien:
la representación del contexto (columnas o dimensiones),
la representación de las palabras (filas de la matriz)
los valores o pesos de cada palabra en cada contexto.
6.5.1. Representación del contexto#
Cada contexto de la palabra será una dimensión de la matriz. El problema es cómo delimitar este contexto: ¿cuántas palabras forman el contexto?, ¿dónde está el límite del contexto?
En el modelo de matriz término-documento que se utiliza en recuperación de información el contexto es todo el documento porque son documentos lo que quieren recuperar, pero se puede limitar a recuperación de pasajes, párrafos, etc. Otras opciones con motivación lingüística podrían ser:
la oración,
una ventana deslizante (un conjunto de \(n\) palabras delante y detrás de la término),
el párrafo o cualquier otra unidad textual,
el capítulo,
etc.
Por otro lado, además de la matriz término-documento que hemos visto (donde las columnas representan documentos y las filas palabras), se puede crear otro tipo de matriz: la llamad matriz de co-ocurrencias o matriz término-término. En estas matrices (normalmente cuadradas), tanto las columnas como las filas representan palabra, y los valores la relación entre esas dos palabras. Por ejemplo, en cuántos contextos aparecen esas dos palabras, como en el siguiente caso:
red readable blue
car 5 0 1
book 3 6 0
Según esta matriz, la palabra “car” aparece el mismo contexto de la palabra “red” en cinco ocasiones (de un total de \(N\) contextos), no coincide nunca con la palabra “readable” en ningún contexto y solo en uno con la palabra “blue”. “book”, por su parte, aparece tres veces en el mismo contexto de “red”, seis en el mismo contexto de “readable” y ninguna con “blue”. En ocasiones estas matrices son cuadradas porque tienen los mismo términos en las filas y en las columnas.
Se pueden plantear otros tipos de matrices. Turne y Pantel (2010), por ejemplo, plantean una matriz Pair-Pattern donde las filas son parejas de palabras \(X:Y\) (“carpenter:wood”) y las columnas son relaciones entre palabras co-ocurrentes (“X cut Y”).
Sea como sea el tipo de matriz, es muy relevante dónde se sitúa el límite del contexto (el documento, el párrafo, la oración…)
6.5.2. Representación de las palabras#
Hasta ahora hemos estado hablando de “palabra” o “término”, pero como ya se vio en temas anteriores, el concepto de “palabra” es muy vago. Una matriz será más o menos representativa según se defina la palabra. Algunas opciones son (según vimos en sesiones anteriores):
el token,
la raíz (o stem),
el lemas,
el lema más la categoría gramatical,
los token pero eliminando stopwords,
solo nombres (o solo verbos, o solo adjetivos, etc.)
el lema más su dependencia sintáctica,
etc.
Algunos de estos casos, como imagino ya sabrás, requieren pre-procesar el corpus con técnicas de PLN. Cuando son colecciones muy amplias, se suele trabar con el token o solo con la raíz de las palabras.
6.5.3. Cálculo de los valores o pesos#
Finalmente, el modelo semántico vectorial puede ser más o menos representativo según se calcule la relevancia (o peso) de la palabra en cada contexto.
El caso más simple para medir la relevancia de una palabra en un contexto es la calcular la frecuencia ponderada: número de veces que la palabra aparece en el contexto, normalizado por el tamaño del contexto. Este modelo tiene, sin embargo, diversos problemas:
Es muy dependiente del tamaño del contexto, que como hemos visto antes no está claro cómo limitarlo. En contexto pequeños se trabajaría con valores muy bajos (ceros y unos prácticamente).
No discrimina la importancia real de cada palabra en el contexto, dado que hay palabra que siempre tienen frecuencias muy alta (como palabras de categorías cerradas, o nombres de uso muy común) frente a otras que siempre tienen bajas frecuencias.
sobre estas últimas, el caso extremos es el fenómeno del hapax legomenon: la mayoría de las palabras de una colección de documntos aparece solo una vez (o con una frecuencia muy baja).
Una solución elegante para determinar la relevancia de una palabra por su frecuencia sin caer en estos problemas es el famoso valor TF/IDF que pasamos a explicar a continuación.
6.5.3.1. TF/IDF: term frequency / inverse document frequency (Sparck Jones, 1972)#
La idea intuitiva que subyace a este valor es que las palabras de uso muy común (aquellas que aparecen con alta frecuencia en prácticamente todos los documentos) no son discriminativas para determinar la importancia del documento. Tienen por tanto poca relevancia en su documento y por tanto su valor debe ser bajo. Las palabras que realmente son relevantes en un documento, las que lo caracterizan, son aquellas que tiene una frecuencia relativamente alta en un documento pero, al mismo tiempo, tiene una frecuencia relativamente baja o nula en el resto de documentos. Esto es lo que intenta modelar TF/IDF: dar más peso a las palabras con frecuencia relevante en unos documentos pero no en la totalidad de la colección de textos.
TF/IDF son las siglas de “frecuencia del término por la frecuencia inversa del documento”. Así, en la fórmula nos encontramos con:
Term frequency (\(tf(w,d)\)): frecuencia relativa de una palabra \(w\) en un documento \(d\).
Document frequency (\(df(t)\)): cantidad de documentos donde aparece una determinada palabra \(w\).
Inverse document frequency (\(idf(d,D)\)): el valor determinante para saber la relevancia del documento es la inversa de la frecuencia de documentos donde aparece. Por tanto, se divide la cantidad toda de documentos \(N\) en la colección \(D\) entre la frecuencia del documento \(df(t)\). Hay varias formas de obtener este valor. La más sencilla es logarítmica, tal que \(idf(d,D)=log\frac{N}{df}\)
Así, el valor tf-idf de la palabra \(w\) en un documento \(d\) en una colección de documentos \(D\) es:
6.5.3.2. PPMI: Point Wise Mutual Information (Church y Hanks 1990)#
Otra alternativa para medir el peso contextual de una palabra muy utilizada en PLN es el Point Wise Mutual Information o PPMI. Así como tf-idf es le estándar para medir la relevancia de las palabras en matrices término-documento, PMMI es la medida que se suele utilizar en matrices de coocurrencia término-término.
La intuición detrás de PPMI es que la coocurrencia de dos palabras en el mismo contexto es relevante en la medida que podamos saber la posibilidad de que ambas palabras coocurran por casualidad. Si no coocurren en el mismo contexto por casualidad, es que esa coocurrencia es motivada y por tanto relevante.
Así, PMMI mide la probabilidad de que dos palabras aparezcan en el mismo contexto, y lo divide por la probablidad de aparición de cada palabra por separado:
Hoy día tf-idf y PPMI son medidas estándar para la representación vectorial del significado. Luego se verán otras propuestas para determinar la relevancia de cada palabra en el contexto donde aparece; pero antes hay que tratar el gran problema de los modelos semánticos vectoriales: la matriz dispersa.
6.5.4. Matriz dispersa y matriz densa#
Dada las características de los idiomas, este tipo de matrices de coocurrencias (bien sean término-término o término-documento) que miden las relaciones contextuales entre palabras son siempre son matrices muy dispersas, es decir, son matrices en las que la mayoría de los valores con cero. Lo normal en un idioma es que dos palabras no compartan contexto. Las palabras que comparten contexto entre ellas son pocas, por lo que lo normal es que el valor entre dos palabras sea cero. Esto es un problema tanto desde punto de vista matemático como computacional: se generan estructuras muy grandes pero muy poco informativas.
Sparse matrix: la mayoría de los valores son ceros.
La solución a este problema es transformar la matriz dispersa en una matriz densa (dense matrix), es decir, una matriz sin ceros donde todas las relaciones entre palabras tienen valor superior a 0. Este problema ha sido el principal interés en la investigación en los últimos treinta año. Vamos a comentar tres soluciones que han tenido especial relevancia.
Una primera solución fue Latent semantic analysis o LSA (Landauer y Dumais 1997). Esta aproximación consigue reducir una matriz dispera en una matriz densa de 300 dimensiones mediante su descomposición en valores singulares (singular value decomposition). Lo interesante de la matriz resultante no es solo que sea una matriz densa; sino que esa matriz densa, además de mantener las relaciones contextuales entre palabras, muestra relaciones semánticas “latentes”: relaciones semánticas entre palabras que a simple vista no se detectan. LSA, así, supuso un avance en semántica vectorial en las tres áreas de conocimiento implicadas: matemática, computación y lingüística.
Años más tarde se propuso Latent Dirichlet Allocation o LDA, que veremos en la segunda parte de la Práctica 1.
Finalmente, la búsqueda de matrices densas y la optimización de la representación contextual mediante vectores ha llevado a los skip gramms, que es la base de Word2Vec y de donde derivan los word embeddings y los modelos neuronales actuales. Para determinar la relevancia contextual entre dos palabras, la idea principal de los skip gramms es entrenar un clasificador con regresión logística que aprenda si una palabra formar parte o no del contexto de otra palabra. Como solo aprende si dos palabras comparten o no contexto, ese entrenamiento no necesita un corpus anotado a mano: basta con una amplia colección de documentos (cuanto más grande mejor). Y al final lo de menos es el clasificador: lo importante son los pesos que ha aprendido para cada palabra. Ese es su vector contextual, que ha demostrado tener gran capacidad de representación semántica. Esto es el inicio del deep learning que se verá en próximos temas.
6.6. Interpretación semántica: distancia y similitud.#
El vector de una palabra en sí mismo no tiene un significado como podría tenerlo, por ejemplo, una definición. Decir que casa es \(\{1, 4, 0, 0, 1\}\) no es nada: ese vector sólo indica la relevancia de la palabra en cada contexto.
¿Cómo se realiza, entonces, la interpretación de una palabra y oración en el modelo semántico vectorial? La interpretación en esta aproximación vectorial a la semántica distribucional se realiza por relaciones de similitud entre palabras, oraciones, fragmentos o documentos. Dos palabras con vectores contextuales similares implica que ambas palabras tienden a aparecer en los mismos contexto, y por tanto su significado está relacionado. Dos palabras cuyos vectores contextual sean muy diferentes implica que son palabras con significado dispar. Cualquier aplicación de semántica vectorial debe pensarse en términos de similitud entre palabras, grupos de palabras, textos, etc. y no tanto como una interpretación sustancial.
La similitud se calcular según la distancia entre los vectores en el espacio vectorial: a menor distancia entre vectores, mayor similitud semántica. Si bien hay diferentes medidas para calcular la distancia entre vectores, las más utilizada es la distancia del coseno, que mide el ángulo entre dos vectores ambos con origen en \(0,0\):

6.6.1. Conclusiones#
Representación formal del significado distribucional.
El significado se represente mediante vectores dentro de un espacio semántica vectorial.
El vector está formado por el peso de la palabra en cada uno de los contextos (documentos, oraciones, etc.). Modelos de representación.
El proceso de interpretación se basa en la distancia entre vectores: similitud.
6.7. Herramientas y recursos#
Para crear espacios vectoriales y calcular similitudes:
6.8. Bibliografía#
Church, K. W. and P. Hanks. 1990. Word association norms, mutual information, and lexicography. Computational Linguistics, 16(1):22–29.
David M. Blei (2012) “Probabilistic topic models” en Communications of the ACM vol. 55 (4), April 2012. Doi:10.1145/2133806.2133826 https://dl.acm.org/doi/10.1145/2133806.2133826
Juravsky y Martin (2020) Speech and Language Processing. https://web.stanford.edu/~jurafsky/slp3/
Landauer, T. K. & Dumais, S. T. (1997). “A solution to Plato’s problem: The Latent Semantic Analysis theory of the acquisition, induction, and representation of knowledge”, Psychological Review, 104, 211-140
Lorenzo, Ferrone y Zanzotto Fabio Massimo (2020) “Symbolic, Distributed, and Distributional Representations for Natural Language Processing in the Era of Deep Learning: A Survey” en Frontiers in Robotics and AI, pags, 153. DOI 10.3389/frobt.2019.00153 https://www.frontiersin.org/article/10.3389/frobt.2019.00153
Navarro Colorado, Borja (2021) “Sistemas de anotación semántica para corpus de español” en Giovanni Parodi, Pascual Cantos & Lewis Howe (Editores) The Routledge Handbook of Spanish Corpus Linguistics Routledge (en prensa).
Widdows, D. (2004) Geometry and meaning, CSLI.
6.9. Cuestionario de aprendizaje#
Una vez realizadas las lecturas, contesta las preguntas de este cuestionario.
